import EoN
import networkx as nx
import matplotlib.pyplot as plt
import scipy
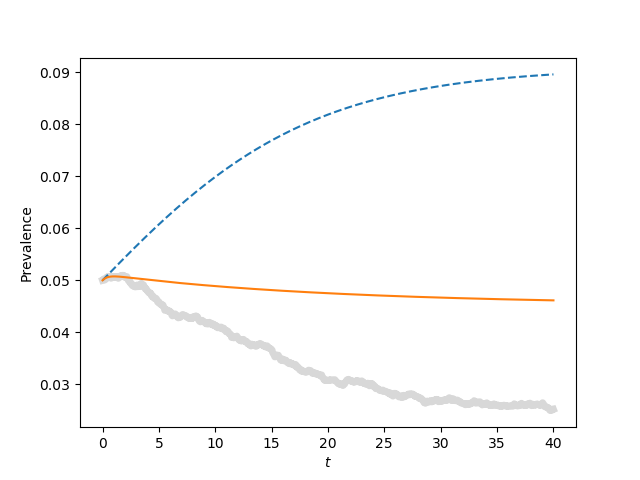
print(r"warning --- plot c in book is mislabeled. It should be \tau = 1.1\tau_c, not 1.2\tau_c")
N=1000
kave = 20
gamma = 1.
iterations = 200
tmax = 40
tau_c = gamma/kave
rho = 0.05
tcount=1001
report_times = scipy.linspace(0,tmax,tcount)
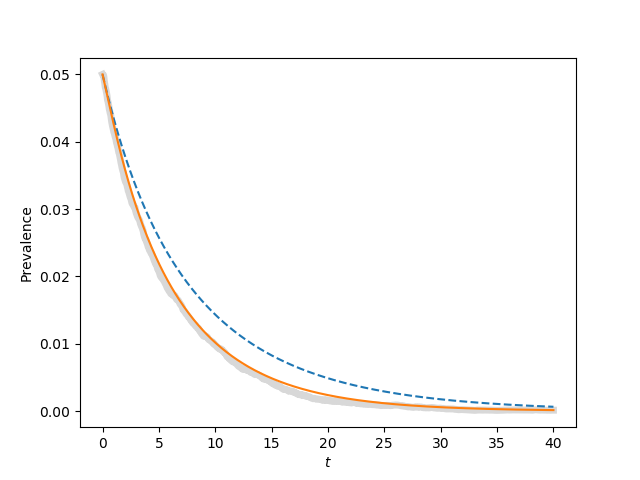
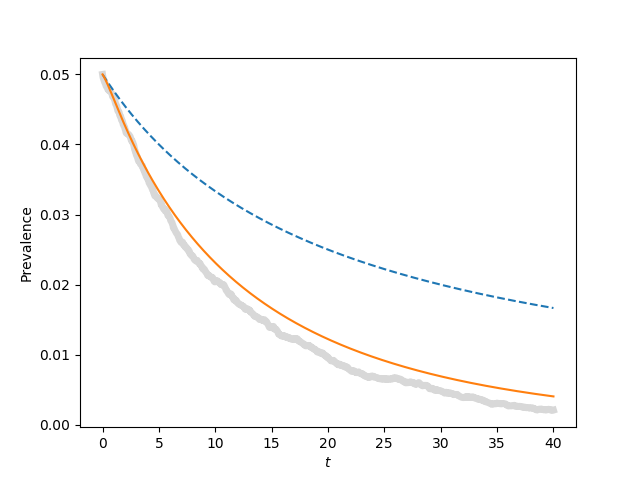
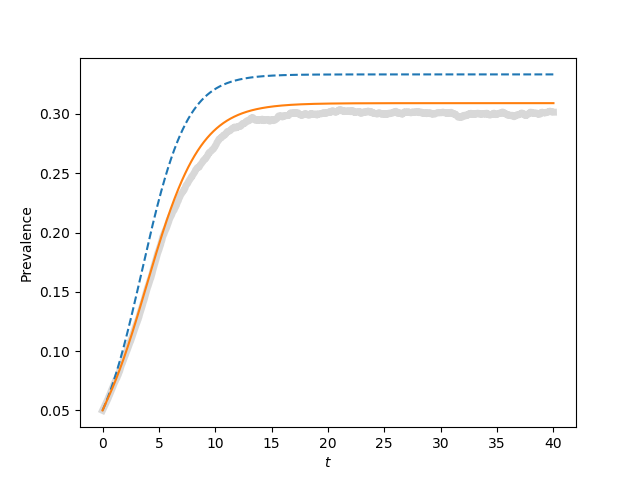
for tau, label in zip([0.9*tau_c, tau_c, 1.1*tau_c, 1.5*tau_c],['a', 'b', 'c', 'd']):
plt.clf()
Isum = scipy.zeros(len(report_times))
for counter in range(iterations):
G = nx.configuration_model([kave]*N)
t, S, I = EoN.fast_SIS(G, tau, gamma, tmax=tmax, rho=rho)
I=I*1./N
I = EoN.subsample(report_times, t, I)
Isum += I
plt.plot(report_times, Isum/iterations, color = 'grey', linewidth = 5, alpha=0.3)
S0 = (1-rho)*N
I0 = rho*N
t, S, I = EoN.SIS_homogeneous_meanfield(S0, I0, kave, tau, gamma, tmin=0, tmax=tmax,
tcount=tcount)
plt.plot(t, I/N, '--')
S0 = (1-rho)*N
I0 = rho*N
SI0 = (1-rho)*N*kave*rho
SS0 = (1-rho)*N*kave*(1-rho)
t, S, I = EoN.SIS_homogeneous_pairwise(S0, I0, SI0, SS0, kave, tau, gamma, tmin = 0,
tmax=tmax, tcount=tcount)
plt.plot(t, I/N)
plt.xlabel('$t$')
plt.ylabel('Prevalence')
plt.savefig('fig4p7{}.png'.format(label))